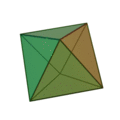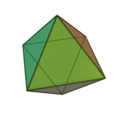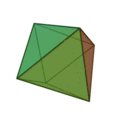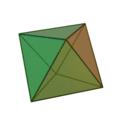
Die fünf Platonischen Körper
(als 3D-Animation; darunter als Abwicklung)



|
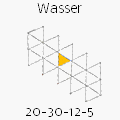
|
mit n Flächen - Kanten - Ecken - Eck-Kanten
Über die fünf platonischen Körper ▼
Sie sind die einzig möglichen konvexen regulären Körper der Geometrie. Sie sind Polyeder, Vielflächner und bestehen aus 4, 6, 8, 12 oder 20 gleichen=kongruenten und regulären Teilflächen. Regulär bedeutet die Gleichheit aller Seitenlängen. Es fällt auf, dass die fünf geometrischen Körper sich mit der Zahl der Flächen immer mehr der Kugelform annähern.
Die damals (seit etwa 6. Jh. vuZ) als Basis-Bestandteile der Welt angesehenen vier Elemente Feuer, Erde, Luft, Wasser wurden bei der Entdeckung dieser geometrischen Besonderheiten mit den platonischen Körpern assoziiert. Das Dodekaeder wurde als Kosmos-Symbol ergänzend hinzugenommen. Warum gerade dieser Körper, ist mir ebenso wenig bekannt, wie bei den anderen Zuordnungen. Platon hat diese PK und ihre symbolischen Deutungen in seine Philosophie aufgenommen und wurde so zum Namensgeber.
Auch diese geometrischen Körper sind Beweis für mathematische Gesetzmäßigkeiten des Alls.
Die in den Animationen der beiden PK-Seiten whervorgehobene Kugelform könnte geometrisch als konvexer Körper mit ∞-vielen regulären Teilflächen (zB Hexa- oder Ikosaeder) bezeichnet werden. Sie vermittelt wegen des Fehlens jeglicher limitierender Kanten und Ecken einen Eindruck von Unendlichkeit: Kosmos.
Das Schema der Beschreibung Platonischer Körper lautet dann:
n Flächen - Kanten - Ecken - Eckkanten: ∞ - 0 - 0 - 0
|
Nähere wissenschaftliche Erklärungen zu den "Platonischen Körpern" durch den Mathematiker und Physiker Walter Fendt. Anmerkungen:
Die weitgehende Intransparenz des jeweiligen Globus kann durch mouseover reduziert werden.
GIF-Animationen: Die Faszination der Bewegung? Etwas bewegt sich, wirkt lebendig, erregt - seit Urzeiten - unsere Wachsamkeit, Aufmerksamkeit. Es könnte ja gefährlich, schmackhaft oder sexy sein... |